Giuseppe Arena - Roger Leenders - Joris Mulder

Understanding memory decay of the relational events in temporal networks

In my project, I work on the tie-oriented relational event modeling framework (Relational Event Model, Butts 2008) and the actor-oriented frameworks (e.g., DyNAM, Stadtfeld et al. 2017). My project’s purpose is to enrich the existing modeling frameworks with new methods (extensions), which aim to understand whether and how past relational events have a different impact on future interactions based on their time recency and other events features in temporal social networks.

This work analyzes email communication among employees from a multinational service company branch. The company's management team organized various events where employees could suggest innovative working methods and offered prizes for the best ideas. The data consists of the time-ordered sequence of emails sent (over a year) among employees and where the exchanged content addressed innovation-related topics. Therefore, we aim to find insights on whether employees have developed an innovation mindset and how differently they have responded to the company's initiative. We achieve this by using the relational event modeling framework and choosing a set of predictors whose estimated effects measure the impact of such predictors on the innovation communication rate. The analysis emerges that innovation communication is more likely among employees working in the same building and generates more from long-tenured employees than from new employees. Employees are more likely to target their communication to employees belonging to a higher hierarchy. Furthermore, in the linear predictor, we also included short-/long-term for both inertia and reciprocity, whose estimated effects measure respectively the propensity towards persistence (choosing to send an email to those actors to which they had targeted most of their emails) and reciprocation (choosing to send an email to those actors from which they had received most of their emails) of employees in selecting the receiver of their next email based on the time recency of past events. The definition of short-/long-term endogenous statistics was our first step at understanding how differently endogenous dynamics might affect the rate of future network interactions. This study provides a straightforward application of the relational event model with a first glance of the not-yet-introduced concept of memory decay in endogenous effects.

Chapter 2: A Bayesian semi-parametric approach for modeling memory decay in dynamic social networks

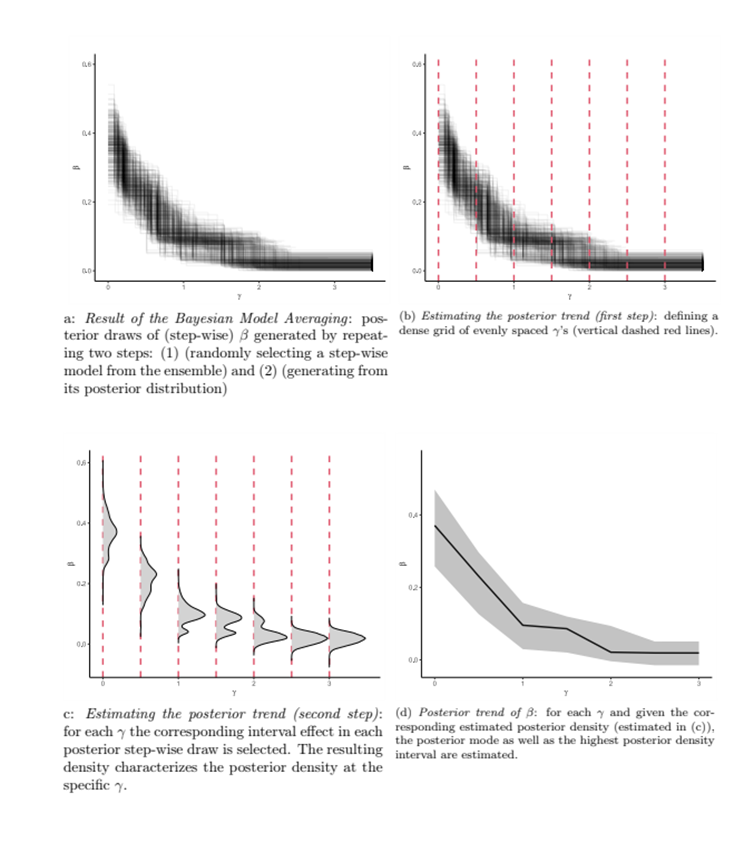
 In this project, we propose a semi-parametric approach that aims at learning the shape of the memory decay from the data and does not require any parametric assumption. We first introduce the step-wise memory decay model and the time interval definition of first-order and second-order endogenous statistics. Then, we discuss the gradual nature of memory decay over the elapsed time. Finally, we introduce a semi-parametric approach that returns a smooth estimate of the memory decay. This approach consists of (1) estimating an ensemble of step-wise models based on randomly generated intervals of the elapsed time, (2) running a Bayesian Model Averaging step to estimate the memory decay over the elapsed time for each endogenous statistic in the model. The four panels describe the approach in the figure.

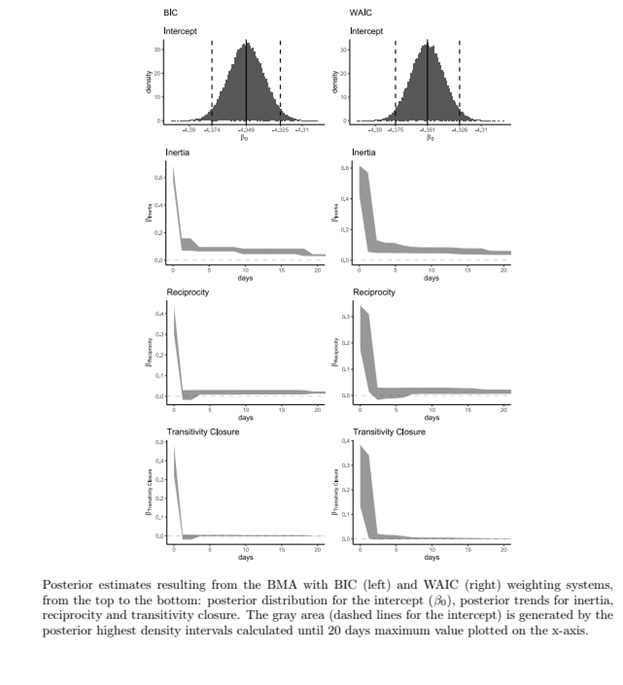
We apply this method to empirical data, consisting of a sequence of demands sent among socio-political actors in India. Though applied to a small set of actors, the study shows the method's capability to estimate memory decay for inertia, reciprocity, and transitivity closure. Results suggest that, on all the three dynamics, actors’ interactions follow an exponential-like decay, and they are mainly driven by events that occurred within the very recent past. Furthermore, we compare the results of our semi-parametric approach with other relational event models where statistics follow parametric decays. We also discuss computational details about the calculation of endogenous statistics and the estimation of the ensemble of step-wise models. The computation of statistics and the estimation stage are optimized, and the routines to run the semi-parametric approach are available within the package bremory.

Chapter 3: How fast do we forget our past social interactions? Understanding memory retention with parametric decays in relational event models

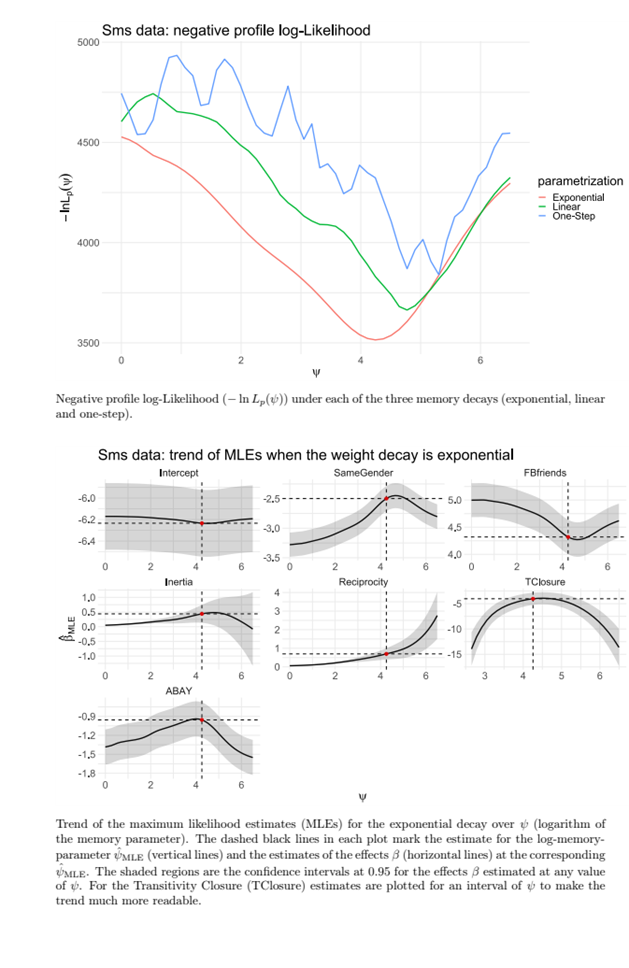
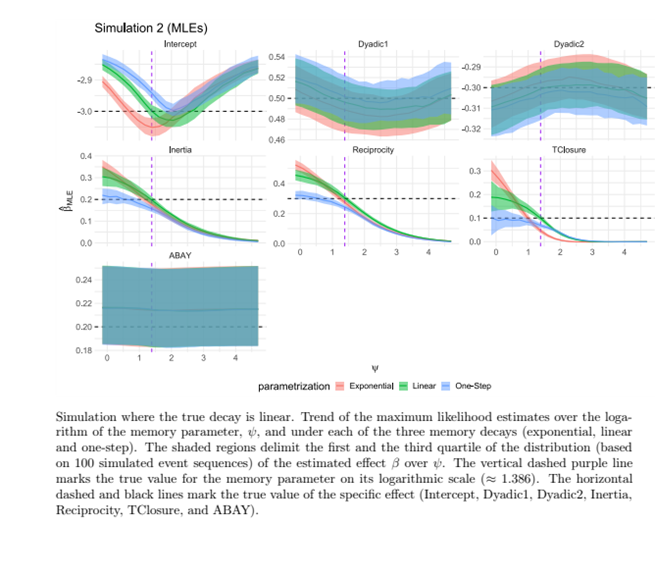
In the third project, we focus on the parametric modeling of memory decay. We introduce three parametric weight decays: exponential, linear, and one-step decay. Then we propose using the Profile log-Likelihood function in a REM with memory parameters embedded in the likelihood and explain the statistical method that helps us decide which memory decay function and memory parameter are the most suitable for the observed sequence of events. We provide results of simulation studies that show the presence of bias in the estimates of effects of the statistics every time that the parametric decay function, as well as its memory parameter, are misspecified. One of the three simulation studies is presented below. The actual memory decay underneath is linear, and models are estimated by specifying three weight decays (exponential, linear, and one-step).

Furthermore, we also test different memory models against each other by using the Bayes Factor. Finally, we apply the methodology to two real case studies: Indian and Sms data. The figure below shows the results for the Sms data application. In the top panel, the negative profile log-Likelihoods of the three models are plotted, and the evidence suggests choosing an exponential decay function. The trend of MLEs under the exponential decay is plotted over the log-memory-parameter in the bottom panel. This plot shows a bias in the effects estimates whenever the memory parameter is not estimated via MLE. Therefore, the estimation algorithm also needs to optimize the log-Likelihood by accounting for memory parameters.  This project prompted us to further develop the methodology around the estimation of memory parameters, for instance: where different event types are present and might lead to diverse memory decays or where memory likely follows a different trend across actors or groups of actors.

Software package

REMSTATS

An R package that provides a set of functions for modeling both tie-oriented (Relational Event Model) and actor-oriented (DyNAM) models. Several optimization methods (frequentist or Bayesian) are implemented to optimize either the log-likelihood or the posterior density of the specified model. In the current version of the package, the available estimation methods are Maximum Likelihood, Gradient Descent, Adaptive Gradient Descent (ADAM), Bayesian Sampling-Importance-Resampling, and Hamiltonian Monte Carlo. I have been working with Rumana, Fabio, and Diana to develop this package.

Retrieve package

REMIFY

An R package for processing Relational Event History (REH) data and arranging them in a new structure used by the packages in remverse. The package will also transform REH data from other formats or other sources to a ‘reh' structure (or vice versa).

BREMORY

an R package containing all the memory-related extensions to REM that I have developed in my projects. The inquiry of how long past relational events are retained by actors and how they shape actors' future interactions is a multifaceted problem. For such a reason, I have been working on creating a package structure that allows the user to have an easy-to-use set of

Papers

Arena, G., Mulder, J., Aalbers, R. & Leenders, R. T.A.J. Understanding employee communication with longitudinal social network analysis of email flows (chapter of an edited book ‘Data Analytics in Action’, Wiley)

Arena, G., Mulder, J. & Leenders, R. T.A.J. A Bayesian semi-parametric approach for modeling memory decay in dynamic social networks.

Arena, G., Mulder, J. & Leenders, R. T.A.J. How fast do we forget our past social interactions? Understanding memory retention with parametric decays in relational event models